Problem statements
Solution video - H26.A
Solution video - H26.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
HOMEWORK 26 - SP 25
16 thoughts on “HOMEWORK 26 - SP 25”
Leave a Reply
You must be logged in to post a comment.
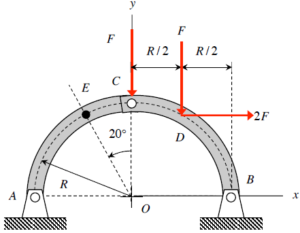
When creating equations for this problem, you are able to separate AC and BC from eachother because they are only combined by a pin, correct?
Also, when it comes down to slicing at E, if you slice the right side off are you only left with Ax and Ay as non-internal resultant forces? Because this is a 2d question there are only 3 internal resultant forces, this allows you to find everything very quickly, but i feel like im missing something.
I believe you can separate AC and BC, so the forces M(at E), Ey, Ex, Ax, and Ay would be in the FBD. However, I'm not sure how to solve for Ax and Ay because there are four unknowns for the overall FBD. Were you able to solve for Ax and Ay?
I solved for Ax and Ay by separating the two arcs into separate FBDs. Taking the moments about A and B in their respective FBDs gave me two separate equations where the only unknowns were Cx and Cy. When you solve for these you can plug them into the force equations on AC to solve for Ax and Ay.
I was able to solve for Ax and Ay using moment equations about A and B for the entire FBD. After that, I focused on the AE member to find Ex, Ey, and ME
Yeah, I believe when you slice at E you are left with Ax, Ay, and MA. This method should be valid to work with, but I could be incorrect.
I solved for both A variables using the moment Equation, after that I used the numbers to solve for the remaining E variables
Can we assume that AC is a 2-force member? I don't see any other forces acting upon it (maybe the F at C though).
Because this problem deals with a semicircle, Ax=Ay and Bx=By. Using this equivalency makes it possible to solve for the reaction forces on A, as there are only 2 unknowns in the full system. When solving for Shear Force and Axial Force, remember to consider the 20 degree cut angle, as it means each respective force has an X and Y component in the equilibrium equations for the cut diagram.
By applying the moment equation at point A to the overall diagram, I was able to determine the value of By. Then, using the equilibrium equations in the x and y directions, I calculated Ax, Ay, and Bx, with the help of a section cut at point C and taking moments about C. From there, it became a straightforward plug-and-chug process at point E—though I made sure to pay close attention to the distances between points A and E along both the x and y axes.
To solve this problem you need to use a lot of trig knowledge. You need to not only find the vertical distance from the x-axis to D to solve for the moments for the entire diagram but also the position of E. After those calculations, it becomes much easier to solve is.
Just to be clear, we are solving for the moment at E, shear force at E, and axial force at E, right? I just want to make sure that I have all 3 in my final answer.
Also, to add to this, would it be permissible to represent both the shear and axial forces as just reaction forces at E? This would mean that my final answer would include both the moment and reaction forces at E. I figured that this would make the problem much easier and less complicated to solve.
That's what I interpreted from the problem. I have my answer as a moment and reaction forces (in vector form) at E
When separating components AC and CB into separate parts and drawing FBDs for them, how do you know where to include the vertical force F that is located along the y-axis?
I believe we can assume that force belongs solely to BC, as described in the given.
Solving using the right side of the cut seemed to be a lot easier.