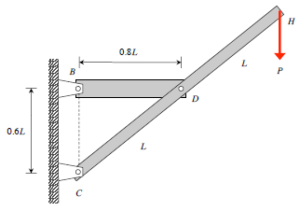
Problem statements
Solution video – H30.A
Solution video – H30.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video – H30.A
Solution video – H30.B
DISCUSSION THREAD

Comments are closed.
What should we have the units be at the end of this problem? Should we convert to MPa or is just Pa fine? Thank you.
They should be fine with either, but since we converted to MPa in class, that’s what I’d do.
For the end of this problem, I did my answer of stress in the units of MPa. I asked the TA’s, and they suggested that we either do kPa or Pa, so I then just converted my answer to Pa. But I think either kPa or Pa would be good.
To find the axial force on member BD, do we start by finding the force in member CDH and then working our way to member BD?
I summed the forces / moments in each member to get the needed equations leading to finding the axial force on BD.
I started with summing the moment through point C
I summed the forces about C to find the axial force on BD.
For finding the axial force BD, I took the approach of summing the moments about point C and finding the reaction for Bx. I assumed this Bx was equivalent in magnitude to BD and then found the stress with this. Is this an acceptable approach or is there something that I am missing?
I believe this is a valid way to solve the problem because BD is a two-force member. This means that Bx is equal and opposite to the force applied on the other end of the member. There should be no need for a CH FBD if you take this approach.
It should be. This is the same approach that I took. I checked my answer with the TA and the numbers matched.
Why can we assume that Bx is equivalent to magnitude to BD?
Would it be possible to find the moment about D in order to solve for the stress in member BD? I am unsure of how exactly we should find the moment about C, as I think the only force that would be acting along the beam would be the load P.
When you create the equation for the moment around C, it will contain the moment from force P and Bx. Since the equation only has one unknown, Bx can be solved for.
When finding the axial force on BD, do you consider both the reactionary force from the B and the reaction from D?
Since member BD is a two-force member, the reactionary force from B and the reaction from D should both be equal. As a result of this, when determining the axial force, the force used is simply just one of the forces.
If the cable in this system were slightly elastic instead of ideal, how would that affect the distribution of tension through the pulleys and ultimately the stress in the cable? Could we still use a static analysis, or would we need to consider deformation compatibility as well?
For this problem are we only considering axial stress or the torosional as well on BD
I would assume we are just looking for the axial stress on the member.
To solve this problem, I began by creating a free-body diagram of the entire system. After this I summed the forces and summed the moments about point C. This allowed me to determine Bx. Next, I drew a free-body diagram of the member BD. Since there were no forces acting in the middle of this member, I came to the conclusion that this part is a 2FM. This allowed me to easily determine the force BD acting on the member. After this, I solved for the axial stress using the values I determined.
For this problem, we are only finding the axial stress in BD given by o = P/A, right?
Also, these comments are saying that units should be MPa. What is the conversion from kN/mm^2 to MPa?
I believe this conversion is 1 kN/mm^2 = 1000 MPa.
To solve this problem, I made separate FBD’s for BD and CH and then used CH to find the tension in BD at D using the Force and moment equations. Then used the tension and cross-sectional area to find the stress.
I also split them up into two sections, and it made the calculations really short and simple. The sum of the forces at x that I got was really straightforward, and I was able to solve this problem pretty fast. Faster than some of the other homework problems.
After separating the FBDs into two, am I correct to assume that the forces in the Y-component of B and D are both zero? Taking the moment around point B seems to indicate so.
If we sum moments around point C to get Bx, can we just say that’s the axial force in BD since it’s a two-force member? And then use sig = P/A with that?
I believe so. I solved the question using that methodology and came to what I believe is a reasonable answer.
Yeap! Member BD can be assumed to be a two force member and then if we sum up moments across C, we only have the moment due to the applied force P and the force at point D, which is in the x direction and can be taken to be in positive x direction. This gives BD. There are no forces to consider for y at B cause of two force properties and at C no reactions need to be calculated I believe because it does not play a role once you calculate force on BD. Then you could just use the stress formula from thereon.
I believe the correct approach is to take the sum of moments at C and then use the result to find the value of Bx in terms of P. This can help us to find the stress in member BD as we have the cross section area as a given.
Unit conversions seem to be necessary for this problem, in order to get the correct answer.
If we draw the free body diagram for CH and use that to take the moment about point C, we can solve for the force in BD directly without needing to find any reactions first. If this is correct, it simplifies the process a lot. From there it’s pretty easy to calculate stress.
Because BD is a two force member, the only force that we care about after we find it is Bx to find axial stress correct?
By recognizing member BD as a two-force member and taking moments about point C in member CH, I can easily determine the tension in BD, since it is subjected to only a single force
Because member BD is a two force member, you know that the force acting on it is completely in the x-direction and can conclude that B_y is 0. This allows you to solve for all unknowns (although you only need B_x to solve the problem).
I also solved this by first finding the moment about c and identifying BD as a 2 force member.
I have found Bx, and I know that BD is a two-force member. How does this help determine the axial force which is needed to calculate the stress?
I found it helpful to treat F_BD as a horizontal force (as it is a two-force member) then apply the knowledge we learned from trusses to solve for F_BD and determining whether it is in tension or compression. One more note, I thought that being careful with the units was helpful on this problem!
I solved this by figuring out that member BD was a 2 force member. Then i took the moment around C to find the remaining forces. Then divided by area.
For this problem, I first drew out two free body diagrams, 1 for each member. Then, member BD I found the moment about B which led me to force Dy = 0. Then, for the member CDH, I did the moment about C to find the value of Dx. After that, I used the sum of the X forces for member BD to find what Bx was, and then used the stress of member BD equation to find the answer. Then converted this to Pa.