Problem statements
Solution video - H31.A
Solution video - H31.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video - H31.A
Solution video - H31.B
DISCUSSION THREAD

You must be logged in to post a comment.
I calculated the stress in each member, and then compared that to the yield strength. I then used the higher stress of my two answers to calculate the FS. However, my factor of safety was higher than the normal range of 1.3<FS<3. In addition, I never used the E given. Did anyone else approach the problem in a similar way?
I think our methods were relatively similar, and you are correct; I don't think E is used anywhere in the solving process.
I also didn't use E anywhere in the problem because the asked nothing pertaining to stress. I also got FS values way above the normal range.
I approached the problem in a similar way and did not end up using the E given to us. I think the E is supposed to be used in relation to stress and strain since it is a Young's Modulus. Therefore I do not believe it is necessary information for solving this.
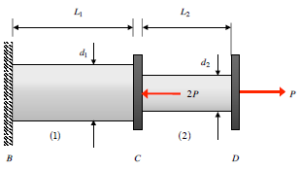
It might be a mistake, but I just want to note the tube that is thinner in the drawing has the larger diameter of 3in. I almost messed that up when I did my work.
The way I solved this question was by calculating the stress in each of the members and then comparing it to the yield strength of YP to determine if one or more of them have failed, and then I calculated the factor of safety.
Do we need the value of Young’s modulus in this question? That would only be needed for axial strain which isn’t asked for, right? Or am I missing something?
I did not use Young's modulus, instead I solved for the stress in each member and based by answer on the factor of safety
I also did not use Young's modulus. I think the E value is only there to prove that the materials are the same and thus, have the same yield strength.
For my solution process I didn't use Young's modulus either. I solved for the stress in each member and then found the FS value for each stress and chose the lesser value to be the factor of safety for the entire rod. I also had values outside the range of 1.3-3.
Since the allowable stress is inversely proportional to the factor of safety, I concluded that the factor of safety of the member with higher stress should be used as it will be the safest option. I do not think that Young's modulus is relevant within the context of this problem as the factor so safety is not directly related to strain. Furthermore, the lectures notes PDF says that the "typical" range is 1.3 to 3 for the FS, but I am assuming that anything outside this range is theoretically and technically possible, but not very typical.
Use d1 = 2in and d2 = 3in for the calculations! It’s what was said in class, even if the diagram looks different—just a reminder
As a reminder, when calculating the factor of safety, make sure to take the absolute value if sigma allowed. This is necessary especially when the stress is in compression.
Yes, it is important to do this step. It is important to remember that a negative factor of safety is not physically possible to achieve.
I did not end up using the value for Young's modulus for this question, which I think was the right approach since we didn't seem to need to solve for the strain in this problem. However, my values I got for the factor of safety were a lot higher than the typical range for most materials, and I'm not sure if I did something wrong or that's just how it worked out for this problem. Did anyone else get a really high value for their FoS?
My FoS was between 1 and 3 (not sure if I can explicitly say the value) but it was way closer to 3 than 1 if that helps.
I also got a very high FoS. I split my FBD into two, used the higher of the two normal stress values, and used the absolute value of strength over stress to find my FoS.
I also got a high value for my factor of safety. I'm glad I'm not the only one with this problem. I split the FBD and summed forces in the x directions. I have no idea what I could be doing wrong. At least there seems to be a consensus that E is not used.
Did you guys use E in your solutions? I got an answer that makes sense but didn't use it. Not sure if I used the right dimensions though.
Vinay, you shouldn't need to use E so you should be good. When you say you aren't sure if you used the right dimensions, what do you mean? You should be able to use the provided kips, and then give the answer for stress in PSI, and then the factor of safety doesn't need a unit attached.
This problem was very similar to the example we did in class. I followed the process of summing the forces in the x direction after sectioning the diagram, finding the stresses from that relationship and relating the resulting stress to the yield point to find the factor of safety. I did not use E to find this.
I did the same thing too. I also followed a similar process that we did in class and was able to finish this relatively quickly. I also didn't use E to find this, but honestly why we might use E to do this assignment.
For part B, I found the factor of safety for each member separately and considered the member which had the lower FoS to be the critical member. I also did not use E to solve this problem.
I never used E in my calculations, and my solution was outside the typical range of 1.3-3 for the factor of safety. Did I miss something? I feel like I was not supposed to be left with pi in the denominator for FS values. Additionally, I was confused about how to draw the forces when taking the sections of the rods. Was I supposed to take a section of rod 1, connector C, and rod 2 as 3 separate drawings or was I supposed to do something else?
I went about solving this how they do it in the example problems where you split the sections down the middle, then do a FBD to find the force. From there you find the stress and then the FoS. My FoS numbers were also outside of the typical range of 1.3-3 using this method so I think that's just how it turns out.
I solve this problem by calculating the stress in each member and comparing it with the given yield strength. I do not use the Young Modulus, but I have a very high FOS for this problem. Anyone has the same issue?
I solved this problem the exact same way. I also did not use Youngs Modulus, and my FOS was high. I believe that is just how this problem solves out.
Would the stress in each be negative if you make forces going to the left negative, or do we take the absolute value of it?
I think that when you get a negative stress you can just say that its in compression, with positive being tension. So i would assume it would be better to take the absolute value so the stresses remain positive in calculations for things like the SF.
I also didn’t use , and I agree with others that it was likely included just to confirm material consistency rather than for any strain-related calculation. As for the unusually high FS values, I think that’s intentional—probably to emphasize the process over realism. Also, the point about sign conventions is key; using absolute values ensures the FS remains meaningful, especially when dealing with compressive stress.
Like the others are saying I solved for the stress of each member to determine if either piece would fail. I didn't use young's modulus either. The diagram is confusing so check your values for calculating the area.
For the FS, do we take the FS of both members and they both are the answer, or is the lowest FS the answer?
I solved the problem by drawing free-body diagrams and finding the axial force in each rod, then used \sigma = \frac{F}{A} to calculate the stress and compare it with the yield strength to get the factor of safety. I took absolute stress values to avoid confusion with compression. My factor of safety ended up being a bit higher than normal, but I think it's just how the numbers worked out.
I did not use L or E for this problem. I believe they gave us quite a bit of extra information for solving this problem. Young's modulus is useful when calculating strain, but not stress.
I see a few comments saying that they did not use E, but did anyone else also not use L1 and L2? I got the final answers but I feel like I missed something important.
I didn't use E or the length of the rods for this question, but I can see that if we were asked to calculate axial strain we might need to use different values than what we did for this problem.
When calculating for each stress load on each member, do we include the negative sign in our calculations? What I mean is for example, the "p" for section "BC" is -2p, which would make the calculation for stress: -24/pi theoretically. But that would give me negative stress.
The sign for the stress calculation can also be seen based on if the member is under compression or in tension and that helps verify the math part.
I find H31.B to be interesting because we can relate it to pistons which are commonplace in mechanical systems. From this problem we can relate it to real world instances where we need to calculate the recommended material for a piston and what the maximum stress/strain it can handle. Pretty cool stuff that makes me excited to be learning engineering.
The problem could actually be started from either side, and by either finding or not finding reaction forces, having tried it both ways. And yeap, L1 and L2 were not given and were not required for me and neither was the Modulus because the question was related simply to the stress, and the related FoS. There was the idea of compression and tension determining the sign which was also required to be in use and as someone said, yes there are direct real world applications of such a problem.
I believe the approach that avoids using E is simpler. Additionally, we can analyze either side after drawing the free-body diagram (though I recommend using both for cross-verification of the results)
For this problem, I began by drawing a free-body diagram for the entire system and then summing the forces to determine the reaction forces. Although this part wasn't necessary, it does help check my answers later. After this, I made a cut in section 2 and considered everything to the right of it. After drawing a FBD and summing the forces, I was able to determine the axial force acting on this member. I repeated this process to determine the axial force acting on section 1. Since the answer I got for the axial force acting on section 1 was opposite of the reaction force at B, I knew my answer was correct. After this, I calculated the areas of the sections to determine the stresses acting on the members. Finally, I used the larger stress value and the yielding stress value to determine the factor of safety on the rod, which was greater than expected.
I also skipped using E and ended up with a higher-than-expected factor of safety
I used similar methods as discussed by other students comments for solving for my FOS and stresses. I used the higher calculated stress for my FOS. I think it's important to note that the normal forces (force used to calculate stress) should be pointing towards the surface the member is interacting with (pointing towards B for member 1 and pointing towards C for member 2).
I found the internal forces using equilibrium, then calculated axial stress with sigma = F/A for both. As others mentioned, I didn’t use E or the lengths since strain wasn’t asked for. Both stresses were below the yield strength so I used the higher one to get the factor of safety.
What would happen if both sections had the same diameter—how would that impact the stress distribution? Would it be evenly distributed?