Problem statements
Solution video – H32.A
Solution video – H32.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video – H32.A
Solution video – H32.B
DISCUSSION THREAD

Comments are closed.
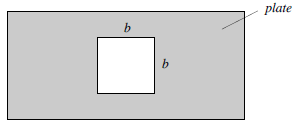
I found this question to be quite simple. I used the shear stress formula and plugged in each value, however, something important to note is that area is the cross sectional area so you have to find the area of the square and multiply that by the thickness of the plate.
I was working through this problem, and I found that the area was the perimeter of the square multiplied by the thickness. The reason why I think it’s this and not the cross-sectional area is because we’re looking for the shear stress which is the stress resisting the force perpendicular to the object (for this problem that object would be the plate).
I also found the area to be the perimeter times the thickness, which is similar to the example problem from class. I agree with your reasoning as well, if you think about the situation it is the perimeter region that resists the force.
I believe that you should consider looking at the perimeter of the square in relation to the thickness in order to determine the area. This is since it is the surface area not the cross section of where the hole is being made.
I also used the shear stress formula to solve it. Just make sure you use the right numbers and factor in that the plate is technically 3d even though its not shown as such in the figure.
While you can technically make an FBD since we’re given forces, it would be pretty difficult to visualize, and the problem is pretty simple. I checked with one of the TAs, and he told me that an FBD isn’t required for this problem.
Right, an FBD isn’t really required here and the formula we use for this is relatively simple. Hence, just using the shear formula is more than enough to solve this.
Even though it is a pretty simple problem, a FBD can be helpful to visualize things. On top of that, it is good practice to draw a FBD for every problem.
The way I solved this question is finding the shear area (which is the the perimeter of the square hole multiplied by the thickness of the plate), and then taking the punching force and dividing by shear area to get the shear stress on the plate.
Yep, same here! I just used shear area = perimeter × thickness, then divided the punching force by that to get the shear stress. Quick and clean method!
Normally in HW’s like these, I tend to just draw out the basic diagram presented instead of drawing an FBD, because sometimes they give marks for having a diagram.
I like to draw out the full diagram or maybe simplify it if there’s a lot going on so that I can see the reaction forces or get a feel for how the forces will work on the structure.
I also thought it was the cross-sectional area at first, but it makes more sense now that the shear area is the perimeter times thickness since the force acts along the cut edges. It’s a good reminder to think about where the material actually fails, especially in 3D cases like this.
It is also important to remember that in the case of circular holes, we would have just done the circumference of the circle (pi*d) multiplied by the thickness of the plate. Since we are using the circumference of a circle, it would make logical sense to use the perimeter of the square in this scenario.
Several of you suggested using the product of the perimeter and the thickness to calculate the shear area instead of the cross-sectional area. Can someone explain why that approach makes more sense in the context of a shearing force
We would use the product of the perimeter multiplied by the thickness as the area in this problem as it is that surface which is experiencing the shear force. The cross-sectional area of the square is what the force P acts on and is not the surface which experiences the shear force. Hope this helped clear things up!
From what I understand, FBD’s are not the focus of this type of problem. Also these simple problems are likely just an intro to the topic, and the exam questions will be more involved. But if this kind of problem were on the exam, an FBD would not be necessary. Nonetheless, thinking about the intuition of why it shears where it does in terms of reactions is valuable.
Are we expected to draw FBD for such simple cases in an exam?
I think we would have to, or even if we don’t it is probably just good practice to. This is because you have to remember and understand that this problem is in 3D even though it is not shown, so they may grade looking for one to check you understanding.
I would not think so since the professor did not emphasize that in class
What units should our final answer be in?
kips/in^2 so ksi I believe
KSI
Using a horizontal view of the hole being punched, I found the area to be not using the perimeter but rather a formula that uses thickness along with the B variable that we get
Can we use Pa for the unit?
Pa is metric units, for this we can use ksi (kips per square inch). You could also convert to psi if you wanted to knowing that 1000 lbs is 1 kip.
Is shear stress = shear resistance?
Not exactly, shear resistance, or shear strength, is a material property that measures how well a material can withstand shear stresses. In this problem, the scope is limited purely to shear stress, so nothing to do with shear resistance. However, if you were determining whether a material would shear if the load described in the problem was applied, you would calculate the shear stress and consider the shear resistance.
For this problem, I found it very useful to start with a FBD of both a side view of the press (as apposed to top-down) and the area that is being cut out to better see the forces at work. It is a very simple problem after that.
The only real hang up I had in this question was factoring in the fact that the sheet is 3d. Other than that, I found the question straightforward, simply using the stress equation.
This is a very simple question (I think, I could be wrong). You first find the area and then you just simply do P/A. It’s simple and easy to claculate.
Just to make sure, the units for the final answer are in kips/in^2, which is the same as kips, right?
same as ksi*
For this one I chose to do kips/in^2. But just to be safe I wrote ksi under it as well.
I used ksi for my final answer as well.
Yes that is the units I used.
I found this problem pretty straightforward. By using the formula, I calculated the shear stress and made sure to use the perimeter of the square hole multiplied by the thickness for the shear area. The units I ended up with were ksi (kips per square inch), which seems appropriate.
For this problem, I used the perimeter area of the hole as the shear area and calculated the shear stress using the given load P. This resulted in a shear stress value expressed in ksi (kips per square inch).
I think this problem is straight forward if you know what area to solve for, it is the area of the material resisting the punch so I found it as the four square made from the side length and the thickness.
I found the question pretty easy. Just make sure to use the right area formula and the shear force equation to solve.
As many have said, it is a straight forward question. On the idea of the formula for area, it is related to the perimeter (circumference if a circular hole) and the thickness as it is usually called because the shear stress acts on that vertical area where that hole I being punches in a sense. That is where the cut is made and hence, the stress needs to be determined for that portion where the hole and the rest of the metal meet/interaction point, and the thickness is because it acts over that whole thickness that it has to cut to. Constantly a force needs until the hole can be punches through. Other than that, the units follow on directly from what is given with kips being 1000 pounds.
Looking at this problem, I think it is best to break it down into the basics and start with an FBD to figure out where exactly the forces are being applied. Doing so shows that there is a force on all four sides of the hole which means the area is going to be perimeter times the thickness.
I believe we should also remember that 1 kip is equal to 1000 pounds. Forgetting this can through your answer off by a significant amount.
*On a complete side note, it’s cool to learn about this since it relates to subtractive manufacturing which Mech E’s will use often in their field. I always find it useful to understand all of the principles behind a process.
I found this problem easier as you really only need to plug and chug with two equations. I was a bit curious as to why it is the perimeter and not the area that is used when calculating the shear force of the object. Since we’re removing a square piece of metal, wouldn’t the resisting material be spread across the whole area of that square?
I like to think of it in terms of a cookie cutter mold. If you were to have a cookie cutter mold that was filled in, the center portion of the mold wouldn’t be able to cut an outline of a cookie effectively (sheer). The cookie dough would spread out from the center (compression) but the sheering would still mainly occur at the edges of the mold. Hopefully that explanation helps.
Although the method of solving is very straightforward, be careful of silly mistakes. Make sure you have the correct units before plugging into the equation and used sheared area for A.
This problem is a fairly simple one. I first began with a FBD to understand the scenario at hand along with the forces acting on the member. I then determined the area that will be used to find the shear stress. This area is the perimeter of the cutout times its thickness. The perimeter of the square is used because this is where the shear force acts (imagine the two parts sliding/shearing across each other). After this, I plugged in the values into the shear stress formula to come up with an answer.
I believe this problem requires the calculation of the area of the hole, then using the punching force to calculate the shear stress. The part I don’t fully understand in the problem is how to calculate the area. I will read the lecture book and research this part.
After some research the area should be calculated by perimeter times the thickness. In this case 4b * t.
This is correct Alexander. Since we’re looking for the cross-sectional area of the shear, and not the area of the punched out section, you should be doing that 4b*t, not b*b.
I agree that is honestly the only hard part about this problem, making sure you remember that the shear stress is located at the edge, which will be the perimeter times the thickness.
For this question I used the equation that used perimeter of the cut out square which was simply B*B. This cross sectional area helped me find the right answer after the force was factored in.
The perimeter of the cut out square would be 4b, right adriaan? Not B*B.
To be able to find the area, it would not be B*B, but instead it be B+B+B+B, multiplied by the thickness to end up finding the shear area. This will help you hone to the right answer.
I believe that for this question the area used in our calculations is the tricky part. We need to use the perimeter of the square (the sum of all four sides or one side multiplied by 4) as this is the section resisting the punch force.
I also used the shear stress formula with perimeter x thickness, makes more sense
Solving this homework problem was relatively easy. To find area, I multiplied the perimeter time the depth, and the rest of the problem can be solved using the given force P and stress equation.
At first, I interpreted the square’s face as the shear area, but when I thought about the material actually resisting the punch, it made more sense that it happens along the sides of the square. So the region where the shearing actually occurs is the perimeter times the thickness.
In order to solve this problem, I first found what shear force, V, was which is the punching force P, aka 60 kips. Then I found the shear area which I did by finding the perimeter distance multiplied by the thickness. Lastly, to get the shear stress, T, I divided shear force by shear area. One issue I had was what units to do, so I chose to do kips per inches squared, and included ksi too.
This problem was pretty simple once I realized what area to use. The shear area is the perimeter of the square hole times the thickness of the plate. I used that in the shear stress formula (force divided by shear area) and got my answer in ksi. Drawing a side view of the setup also helped me see how the force was applied
For this one it was helpful to draw the cross section and think about the force applied across that since the shear would impact the actual thickness cross section