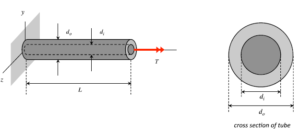
Problem statements
Solution video – H33.A
Solution video – H33.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video – H33.A
Solution video – H33.B
DISCUSSION THREAD

Comments are closed.
When calculating the maximum shear strain in the shaft, is it appropriate to use Hooke’s Law for Shear to calculate shear using the found strain and the given G value? Or is it necessary to make adjustments to the formula because it is torsional loading?
To calculate the shear strain, I believe you are asking as to if you can directly use the shear stress = G*shear strain formula or does it change? You used the torsional loading idea in calculating the shear stress initially right?, and so that shear stress you calculated is due to that torsional loading. And hence I believe, you can use just that general formula because you have already calculated the stress given the applicable loadings on the shaft. And that stress strain relationship follows the law for any linear material of this kind in the elastic region.
Hey Prakhar, yeah that makes sense. Since the stress is from torsion and the material’s elastic, we can use t/G to get the shear strain. And like you said, it’ll be max at the outer surface. Just plugging the equations in should work.
Based on content from earlier in the chapter, shear stress = shear modulus * strain. Therefore, I believe you can use this relationship to find the proper strain by dividing stress by the shear modulus. My only thought on adjustments would be that you would need to properly convert any measurment units before using the equation.
When I was calculating the shear strain in the shaft, I did not use Hookes law, but instead I used the equation where you divided the shear stress by the materials shear modulus. This should give you the correct answer for shear strain with the units rad, and would probably be easier because we already found one part of the equation and are given the other part within the prompt.
I found that this problem was relatively straightforward since it was practically the same as the questions we worked on in class. I just took the equations for stress and strain and plugged in what was given to find the unknown.
Is there anything tricky to look out for? I did it and it seemed relatively easy so I just wanna make sure.
The only tricky thing to watch out for would be units, make sure that everything is either in ft or in. Other than that this should be rather straightforward.
I also used the equations from class and applied it to this problem. I found that visualizing the tube as an actual tube helped me alot to find the shear strain. I imagined it was one of those pool tube floaties which sounds silly but actually helped me solve the problem.
This problem is very similar to the book examples and is a nice application of the equations that were learned in class. Seems pretty straightforward but make sure to realize that it is not a solid filled in shaft
This problem has an example worked out nearly exactly like it in the textbook, so its pretty straightforward. Its a pretty solid example of the relationship between stress and strain and provides an effective method for visualizing the forces within the shaft.
When we say where the maximum shear stress/strain is located on the cross section, do we say it is at a specific point or at all points at a specific radius from the center?
In the case of the maximum shear stress and strain, they both occur along the shaft’s outer radius.
why not the inner radius?
I just looked at the formula for shear stress. The bigger the radius, the larger the stress, which means that the max stress should be at the outer radius. Shear strain is also proportional to shear stress, so it should be the same there.
The shear stress/strain is directly proportional to the distance of the point from the center of the shaft, and that’s how I figured out where the it will act. Apart from that, straightforward problem using the equations we learned in class.
When calculating the shear stress for part a, do we need to convert the torque from kip-ft into inches or can we leave it in ft?
I believe we need to convert it from kip-ft since everything else is in inches. They were definitely trying to trick us!
When you convert from ft to inches, the units work out to be ksi, which is what we want when solving for shear stress.
In order to calculate the maximum shear stress, will we need to calculate the polar moment of inertia?
I don’t think you would need to calculate the polar moment of inertia, but I could be wrong. Though, the way I did it, I didn’t use polar moment of inertia.
There is no need for that
After I realized that the inner section of the tube was hollow, the problem became fairly straightforward. To calculate the maximum shear stress, i used the equation we learned during class. It is important to note that the maximum shear stress and strain occur on the shaft’s outer radius since they are both proportional to the distance of the point from the center of the shaft. For the shear stress diagram, I found the example we did in class to be very helpful. To calculate the shear strain, I used the equation that relates the shear stress and strain through the value G.
This problem was pretty similar to the ones we did in class, so it felt straightforward. Once I remembered the shaft was hollow, I used the stress and strain equations with the given values. Since stress and strain increase with distance from the center, the max happens at the outer radius. The class examples really helped with the shear stress diagram too
One thing to look out for is that when making the graph in part B, you need to make sure that the shear stress is a distributed load and not concentrated on a single point. It reminds me of the graphs we made with water pressure.
I think you can just use the shear stress = G * strain formula since the stress comes from torsion
For this problem, I calculated the shear stress using the formula that includes the applied torque, the outer radius, and the polar moment of inertia. Once I found the shear stress, I used the relationship between shear stress, shear modulus, and shear strain to solve for the shear strain. I also made sure to carefully check the units throughout the process to ensure consistency throughout the entire calculation
When calculating shear strain for a hollow shaft under torsion, does the thickness of the wall affect how strain is distributed across the radius, or is the maximum always at the outer surface regardless of thickness?
Hi Hamza, the maximum strain is still at the outermost surface. The strain is distributed differently in a hollow tube, but I don’t think it matters in this question.
Be careful to use consistent units when performing calculations.
When starting to solve this problem, for part a, we had to calculate the max shear stress. I did this by using the equation =(T * ro) / ((pi/2)(ro^4 – ri^4)), where we would also have to convert T to inches bc it is currently in kip/ft. After getting this number, you can use it to solve the max shear strain, part c. This is done through the calculation of max shear stress divided by G, which is the shear modulus for the shaft material.
I did this similar to the way we practiced in class – converting the torque first (from 60 kips-ft to 720 kip-in) so every term is in inches. Then, computing tau max = T r / J with the outer radius since the tube is hollow. Then, using hookes y = tau / G, I got the strain because our tau max was known.
This problem is very formulaic, the only “trick” is to make sure your units are correct for maximum torque. The maximum shear stress proportional to r so it is fairly easy to determine. The last part is just the same as the relationship between normal stress and strain.
Why does the maximum shear stress in a tubular shaft occur at the outer radius rather than the inner radius?
I was confused about the same thing. I believe the maximum shear stress occurs at the outer radius because of how torque is transmitted through the shaft’s cross section. The farther from the center, the more the material has to stretch around the axis.
This problem is pretty straightforward due to the formulas. The hardest part for me was figuring out how to draw the diagrams. I didn’t exactly know what direction or where to put the arrows. Additionally, keeping units consistent was kinda hard to kepp track of.