Problem statements
Solution video – H34.A
Solution video – H34.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video – H34.A
Solution video – H34.B
DISCUSSION THREAD

Comments are closed.
I found this problem to be relatively simple, I just followed the solving process of the various examples we did in class. As with most of these problems, it is important to remember that the given value is the diameter but the equations use the radius, so dividing the diameter by two is important. Other than that, there isn’t much to worry about when solving this.
I totally agree with you, I found thinking in terms of radius instead of diameter makes it much easier when plugging into the stress formulas. I also found that once you break down how the torque gets passed through each section, it actually clicks pretty well. Especially with part b with shear stress.
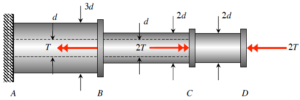
I also agree, the problem was pretty straightforward. How I solved this was first dividing the diagram into individual parts, a total of 7 sections, and wrote out the forces for each one. Then for rigid connectors B, C, and D I found the moment equations for them to determine what T1, T2, and T3 was. Based on these values, diameter values, and if the shaft was solid or tubular, I found the max shear stress for components 1, 2, and 3, then determined what the max one was.
When solving this problem, should we leave the answer in terms pi? Or should we just round to a number of decimal points?
I think either should be fine, though I left mine in decimal form.
I think either form is fine.
I would leave it in terms of pi since it makes it easier to compare the shear stress between the 3 components and it’s just less work that way.
I would leave it in terms of pi as it is a more exact answer but i think either is fine.
I believe either or should be sufficient. Personally, I leave my answers in terms of pi to reduce the chances of rounding incorrectly.
When I solved this problem, I thought it would be best to leave the answers within terms of pi. This is because it is simpler looking and easier to understand and compare quickly, by only comparing the numerator, instead of having to divide out the number, determine sig figs, rounding, etc. So, in terms of pi should be good.
How do we calculate the torque load on each member, do all of the torques affect each member or is it just the torque that is touching the member?
When I solved this problem I only considered the individual torques that each member maintaines themselves. I did not sum all of the torques for each member. I believe this is because the torque load is internal to each component.
Think about the reactions at each end of each segment, and that there has to be an equal and opposite torque on the rigid connectors. Also draw the applied torques according to the drawings. Then write equilibrium equations for the torques at each connector and solve for the torques at each member.
I drew free body diagrams for each connector and solved for the torque loads on each component using these. If you start at connector D and work your way to the left, you can solve for the torque load on component 3, then component 2, and finally component 1.
For this problem I made sure to keep in mind that the first two components are hollow tubes while the last one is a solid one. This is very important as it alters the shear stress equation one has to apply, particularily when solving for the J component of the equation. I’d say keeping this in mind is the only really diffiuclt part of this assignment.
I found the video from HW33.A and the examples we did in class very helpful in solving this question. I determined the location of the max shear stress by finding the shear stress in each member (keeping in mind the difference in the tubular and solid cross sections), then seeing which one was the largest shear stress to determine where the max shear stress occurs.
I also used HW33.A to help me set up the problem. My initial setup right, but I realized later that I messed up the direction of one of the torques, which threw off my results. Definitely a good reminder to double-check the torque directions when drawing FBDs.
The video for HW33.A really helped me out with this one since it covered a pretty similar situation. I focused on finding the shear stress in each part, making sure to remember the difference between the solid and tubular sections.
I found it really helpful to sketch a free‑body diagram for each tube segment—just to make sure I wasn’t accidentally summing torques that don’t actually act on that member. I mixed up mm and m halfway through my calculation and ended up off by a factor of 10³ until I did a unit check, which is important to look out for.
I found it easier to find the magnitude of the troques involved on each segment by drawing the torque free body diagrams for the connectors and the segments. That way, I was able to solve for the necessary loads and determine the shear stress & find the max(stress) by comparing the torque loads. I also think that using the magnitude is sufficient for the shear stress, but I found it helpful to account for the signs initially to end up with the correct magnitudes after summing the moments.
Drawing the FBD’s for each shaft segment helps clearly identify the internal torques. Using the signs initially ensures we apply equilibrium correctly, and then comparing the magnitudes makes it easy to find where the maximum shear stress occurs because it is proportional to torque.
Do be careful with the fact that the first two sections are hollow, but the third section is fully solid. Also note that the values given in the problem is in diameters. To find the torques, I first started with an FBD to find if a torque at A, and then use that figure to find the torque for all three sections.
I agree. We should be careful about the first two sections because I made a mistake in assuming which parts are hollow and which aren’t. I also lost a good chunk of work because the values are in diameters and I didn’t divide them by two to get the radius. Otherwise this homework isn’t too bad, but we just need to be really careful in assessing the problem.
I found this problem to be pretty straitforward, the best resources for solving this problem were the video for 33.a and the formulas provided in the lecture notes. I also left my answer in pi to keep it more exact since we are not given the values of t and d. Drawing each fbd for each section was very helpful to keep the signs straight to get the right moment
I forgot to use radius instead of diameter when I first did the problem. Also, don’t forget to make FBDs of each individual component. When solving keep in mind that AB and BC are tubes, so that will impact the stress calculations.
For this torsion problem, I’m unsure how the rigid connectors at B and C affect the torque distribution in each component. Any insights on how these connections influence the internal torques?
I think it’s assumed that the connectors distribute torque evenly across the connected components.
Similar to the solution video for H33.A, you can draw free body diagrams for the connectors and use these to solve for the torque load on each component. If you start with the rightmost connector (D), you can solve for the torque load in component 3 and then keep working to the left to solve for the torque load in components 1 and 2.
How would the internal torque in each section change if an additional torque was applied at the midpoint of component (2)?
Be careful not to confuse the diameter with the radius, and make sure to check whether there is any empty space inside.
Make sure to convert diameters to radii before using the torsion formulas. Since AB and BC are hollow, I used the correct J formula for tubes
If you are struggling on this one, watch the solution video for 33.A. The problem is very similar in that there are torques applied to segments of a rod with different radii joined with rigid connectors. However, pay attention to the fact that two of the segments are hollow, so the max shear stress equation will be slightly different. Use the same method as the last homework to handle the hollow shafts, but other than that, follow the process from the video.
I found that this problem was solved essentially the same way as the examples we did in class. The only thing I needed to focus on was making sure I didn’t make any arithmetic errors.
I solved the problem by calculating internal torques using equilibrium at each connector, then applied the formula for hollow shafts from class to find shear stresses in each of the three segments to determine in which shaft the maximum stress occurred. Overall relatively simple if following the formulas from class.
For this problem I believe that a solid starting point is to calculate the internal torques like we did in class then use those to solve the problem. Just keep in mind that one of the shafts is solid while the other two are hollow.
Is anybody getting zero torque acting on member 2? I keep looking over my calculations just to check my reasoning, but the value just isn’t making sense to me.
Yeah, I’m getting the same thing. It makes sense because the 2 torques on the right are of equal magnitude and opposite direction, meaning they will cancel each other out.
I thought the video for HW 33.A was really helpful. It made me realize how useful it is to draw free body diagrams for each connector when figuring out the torque on each part. Also, while calculating the max shear stress, I made sure to check whether the cross-section was solid or tubular since that changes the calculations and formula quite a bit.
The method to solve this was pretty straightforward, simply dividing into multiple parts, solving for separate moment torques and then identifying each max sheer stress for each component. The maximum sheer stress for a tubular cross section is at the inner surface.
Why does it matter whether the shaft is hollow or solid when calculating shear stress
It matters because the polar moment of inertia (J) depends on the shaft’s geometry. Think of it this way: a hollow shaft has less material resisting torsion, which means that it will experience a higher shear stress for the same torque.
You look at the free-body diagram of each shaft segment. Start from one end (like point D) and work your way across. Add or subtract torques based on their direction (clockwise or counterclockwise). The internal torque at any segment is based on the net torque acting up to that point.
Like others are saying on this thread the video for HW 33 is very helpful since the situation in both are very similar and you can use the method to solve this homework. The main difficulty with this problem is signs so make sure to carefully mark down signs to not get confused.
I started by drawing FBDs for each shaft segment and connector, which really helped me track how the torques were being distributed. One key thing to keep in mind is that the first two sections are hollow, while the last one is solid so make sure to use the correct formula for J in each case. I also double checked that I was using radii, not diameters, before plugging into the shear stress equation.
Two things that I kept in mind while doing this problem are that shear stress equations use the radius (not diameter like we’re given) and that two of the components were hollow while the last was solid – this changed the formula for J. Using the correct geometry and having calculated the internal torques made it easy to compare the stresses among the components.
One could work this problem from either side by starting with sections from the free end, or overall first calculating reaction force and then so on and so forth. FBDs could also be of multiple kinds based on what I tried and saw, and overall they give the same answer. Some parts to keep in mind though for sure are the signs for the torques and the diameter and radius usage.
One of the biggest things that helped me to determine the location of the highest torque is to think about where in each of the possible components, the highest torque would be exhibited. This helps you to narrow down a lot.
When solving for the torques in each component, you can use the moment equations about each of the rigid connectors. With these values you can use the sheer stress formulas for tubular and solid surface areas respectively.
I found video one very helpful for the first part of the question in order to find the values for A (torques). I personally started form the free end and worked my way back to the held end. For B I used the second video uploaded in the extra learning section as it had an example that was sort of similar and used the same equations as are needed in this problem.
How would one go about finding the location of the maximum shear stress? Would this be done in a similar manner as the graphs we learned to make earlier in this unit and then using this to determine where it’s at its maximum or is there a better method?
You can use the formula for max shear stress using polar moment, radius, and max torque.