Problem statements
Solution video - H24.A
Solution video - H24.B
DISCUSSION THREAD
Please post questions here on the homework, and take time to answer questions posted by others. You can learn both ways.
Problem statements
Solution video - H24.A
Solution video - H24.B
DISCUSSION THREAD

You must be logged in to post a comment.
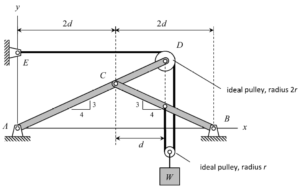
Does the force of the weight apply to the point of connection on the bar BC or does it apply to the joint D.
It should apply a force in the -y direction at the point of connection on bar BC. It also applies two forces to joint D in the -x direction on the top of the pully and in the -y direction on the right side of the pully. However, if you make FBD for each bar, they will be in separate FBDs.
Think instead about how the cables attach to the frame, and what that tension is in the cable due to the weight, then you'll know the force at BC and joint D due to the cable attached to the weight
Im pretty sure the force applies to both BC and the pully so BC is not a 2 force member
I think that the force of the weight does still apply to the BC bar because of the pin on the member. This would mean that BC also can't be treated as a two force member in this circumstance.
It should apply at the point of connection on bar BC and at point D. The weight of the block will have a negative force in the y-direction on the bar, BC. It will also exert a negative force in the x and y direction at point D. These forces will become clear when separate free body diagrams are made for each of the members.
The weight only applies to the box being held by the pulley-which then the tension from the pulley acts on joint D. The weight however doesn't apply specifically on joint D or bar BC.
The weight is just a force in the -y direction. So it will apply a force to anything that its involved with in the calculations. In this case both the bar BC and the point D.
The weight force acts downward on the connection point between the weight and bar BC. It also exerts forces on joint D, but these are considered separately in individual FBDs.
I said that it applies a force to both BC and D.
I'm confused about the forces at D. Is it correct to say that half of the weight of the block acts in the vertical direction at D? Does the force at D have a horizontal component?
I think this depends on how you are going about the FBD. The way that made the most sense to me was to separate the forces at D into the forces on the pulley. In this case, yes there would be a tension force pulling down on the edge of the pulley that is equivalent to half the weight of the block. There is also a horizontal force pulling on the edge of the pulley in the direct of point E because point E is providing tension in that direction as well. Once again, this force should be equivalent to half the weight of the block. If you do it this way though, be careful of your dimensions, these forces are acting on the edge of the pulley, not the frame itself (so you have to consider the difference in length caused by the radius 2r).
I dont fully understand how the radii cancels out. The FBDs are initially in terms of d and then doing any equilibrium equations considering the radius r would have it so they don't cancel anymore as there is no relation between d and r. I thought in a pulley system like this you just assume the force acts on the point at the center of the pulley but realize that is also likely wrong. Also, do we consider the distance that the weight is off center from the tension in the cable or assume the weight is acting on the same line.
If you find the moment about a point along the bar AD, the two pully forces at D have opposite signs. This means when you find the force at the distance, one pully component will be a negative force * (distance1 + radius) and the other pully component will be a positive force * (distance2 + radius). When simplifying the equation, the rs will cancel out.
At D, there is a vertical and horizontal tension that is located around or on the edge of the pulley. When finding the moments around A, you need to include the radius of the pulley plus the horizontal or vertical distance. When you simplify the sum of moments around A equation, the r value will cancel out, since the moments caused by the tension at the pulley are opposite sign.
Yes, reviewing pully systems you can see that the ratio of the weight is relative to the sin of the angle of wrap. Since the pully at the bottom has a wrap of 180 degrees the tension on each rope will be 1/2 of the weight, and because the top angle is 90 degrees there is the same tension on each end of the pully.
Yes D should have both a force in the vertical direction and the horizontal direction, both of which would be w/2.
I think since it's an ideal pulley you can divide the vertical force by two because the force is split by the smaller pulley. As far as horizontal forces at D, I believe there is one that corresponds to the reaction force on E since the pulley is attached to the pin at E by the cable between them.
I would say no, at the point D there should be horizontal and vertical components of the force acting there, Dx and Dy. The force caused by the weight is acting on the outside of the pulley and that is where it is applied not directly on the point D.
Does the horizontal force created by the pulley system need to be considered for rigid body equilibrium or is it a force internal to the system considered only with the links?
In our isolated FBD's, how do we know if a certain force is Fx, Fy or a single force in the direction of the element?
If you are asking about the reaction forces occurring at point C, we are to treat it as a pin reaction so it has an x and a y component.
When drawing the isolated free body diagrams to draw the reaction forces or whatever force we are trying to find, in the case of point C it breaks off into two separate free body diagrams and so on the diagram with A C and D you would draw the C x and the Cy in the direction of C B, the same goes for on the Free body diagram for CB, you draw the forces in the direction of A C D.
If a member has a force being applied to it somewhere on the member other than the joints, or if a member has more than two joints, you must treat it as a multi-force member and break down its forces into Fx and Fy components.
Does the force of the weight apply to Joint D?
The force on joint D isn't W, but it's equal in magnitude to the tension of the left string of the pulley holding W.
Yes; but the force on the pulley is only half of the weight since the other "half" of the rope is attached to CB.
Yes, sort of ... the weight applied at joint D is equal to 1/2W. This is because the pulleys are ideal pulleys, and the weight on one side is equal to the weight on the other
Do we need to consider the radii of the pulley, or are they not applicable to the problem because we are focusing on A and B?
Yes you do, but the radii should end up cancelling out so you can still have an answer in terms of W/
Yes, you always consider the radii when working with pulleys!
Yes, you would have to use the radii of the pulleys in your moment equations.
Is it safe to assume that the tension in the rope is equal to w/2?
I believe so. The smaller pulley allows the tension force to be split evenly along the two members to which it is connected. The tension of the rope attached to the left wall will be the same as the tension just on the other side of the pulley.
Yes, as in the small pulley basically 2T holding W, and with total force on the pulley in the y direction is 0, it becomes 2T - W=0 and T = W/2. and as the rope is the same for both small and big pulley, T is going to be W/2 for tension at both pulley.
For point D, is the tension force for DE also equal to w/2 since the tension force of DE and D is the weight of the same string?
I think so, because the pulleys are ideal so the forces from each end will be identical in magnitude. And since the tension on the string pulling down on D is W/2, the tension on the string pulling left on D is also W/2.
Do we need three separate FBDs?
I originally had three FBDs, but I ended up only using two of them (members AD and BC), as the force from the pulley (T=w/2) is projected onto point D and a point between C and B. Because of this I think you can get away with only drawing two of them as all of your forces are present. From here I found the moments at B and A and then made equilibrium equations for both FBDs.
I only ended up using 2 FBD's, one for member AD and one for member BC.
If taking a moment, how do we find the vertical distance? We only have the horizontal distances.
They put 3/4 triangles for AC and CB so I used those to find the vertical distances
For the overall FBD, there is a horizontal tension and vertical tension at point D, but do we also need to consider the force at the midpoint of CB due to the rope attached there?
Yes, the force provided by the weight is split between the two ropes, so there is also a downward tension force acting on CB
Do we have to find the moment around A and B to start the problem?
Yes, I started the problem by calculating the moment about point A, which helped me solve for the y-component of the reaction at B. Then, you can use that value to calculate the y-component for the reaction at point A. From there, you have look at each member individually to calculate the x-component of each reaction force.
Yes ! That would be the best way to begin. By solving for the moment at A and B then you can solve for cy and cx which would let you acquire the reaction forces at ax,ay,bx, and by! Hope that helps!
I'm starting by finding the moment around point b, how does one find the lever arm for Cx?
Since we are given that the CB member has a slope of 3/4 (shown by the triangle on the member with 3 in the vertical direction and 4 in the horizontal direction), we can multiply the horizontal component of 2d by 3/4 to find the moment arm for Cx to be 3/2d.
I said that my Force Bx is equal to Force Cx, but now I am double-guessing my assumption. Can someone help me figure out why/why not? I followed a pattern to a similar practice problem and they assumed this.
I found that Bx is equal to Cx by using my free body diagram of the CB member. I found the sum of the forces in the x-direction to be Bx - Cx = 0, meaning that Bx = Cx. I assumed the Cx force was in the negative direction to compensate for my assumption that Cx on the FBD of ACD is positive.
I’m wondering if we include the Ey in this equation at point E since it is at a joint, yet, we don’t really use it. Is it really necessary in our calculations I’m wondering.
For me, the easiest way to solve the problem was first solving for the tension in the cable compared to W. Then apply that tension to the pulley at D to find Dx, Dy. Also make FBD for each member, and then one of the entire machine with the external forces. Then you can take moments, sum(Fx), sum(Fy) of various FBD's till you get the needed reaction forces.
What forces are attributed to the moment of point A for the entire FBD?
When you take the moment of point A you only include the forces shown In the main picture, the Cx and Cy will only be included in the FBDs of the split trusses because they cancel each other out when acting on each other in a main FBD. Taking the moment at point A will leave too many unknowns to solve, therefore slicing the FBD to create Cy and Cx will create a moment and Fx and Fy equation that can be used to solve the unknowns.
Why would you need to include the radius in the distance for the moment equation?
You would need to include the radius in the distance for the moment equation because the force is not acting directly at the point. It is acting on the wheel at a distance of the radius from the point, and therefore that distance would need to be factored in when solving for the moment. You will find that the value of the radius will cancel out with your sum of moments calculation though. However, it is still important to be considered in your moment equations.
for problem A what is the connection at point C. if it is a pin how does that it not flip up?
I'm a little confused since if the bar in problem A is connected to the wall at point E, shouldn't the incline slope have no bearing on the reactionary forces?